“The Dirac Distribution and Empirical Distribution”

↑ は、Goodfellow本 3.9.5節のタイトルです。Empirical Distribution が「経験分布」です。

経験分布はデータのサンプル（=観測・経験）集合の確率分布です。最尤推定はつまるところ、この経験分布と想定されるモデルの分布（正規分布、ベルヌーイ、カテゴリカルなど）の間のKLダイバージェンスを最小化するように訓練することです。そしてKLダイバージェンスを最小化するということは、交差エントロピーを最小化することと同じです。（この段でMSEは経験分布とガウス分布をモデルに仮定した場合の交差エントロピーだということがわかる）（ Goodfellow本 5.5節あたりに書いてある)

何が言いたいかというと、経験分布とモデル分布の比較として最尤推定を捉えれば、回帰・2クラス分類・多クラス分類の”各種”誤差関数の根っこは同じになって、全部一貫して理解できるので、嬉しい、ということです。

ESLの2.4では統計的決定理論として、経験分布と予測分布（=>モデル分布のこと）の誤差として、最小二乗法と最近傍法を一般化する形で説明されてます。

このあたりの首尾一貫した統計的学習理論は、僕みたいにエンジニアとして予備知識なしにハンズオン系の機械学習本から入った場合、少なくとも初回は全く素通りすることになってしまい、例えば最小二乗法と最近傍法は全く別の「ツール」として頭に入ってきて、先に進むにつれてそんなツールがひたすら増えて、もうダメです状態になります。何度か諦めながら色々と手を出しているうちに線がつながってくるのですが、結構時間も無駄にします。ただ、誰かが組んだカリキュラムに沿って最後まで登り切る忍耐もないし、結局いろんなところをうろうろしたうえで、来るべき時期が来ないとつながるべき線もつながらないという。まぁそういうもんですかね。。。

話がそれました。そんな経験分布ですが、

経験分布は、
ディラック分布を構成要素としていて、
それはディラックのデルタ関数により確率密度関数として定義される

なのですが、読んでるだけだとそもそも３のディラックのデルタ関数のピンが来ない。理解のためにこんな感じかという実装をしてみました。

サンプルが正規分布してるとして、

import jax.numpy as jnp
from jax import random
import numpyro.distributions as dist
import matplotlib.pyplot as plt; 
key = random.PRNGKey(49)

normal = dist.Normal(loc=0.5, scale=1.)
samples = normal.sample(key, (1000,))
plt.hist(samples)
plt.show()

dist

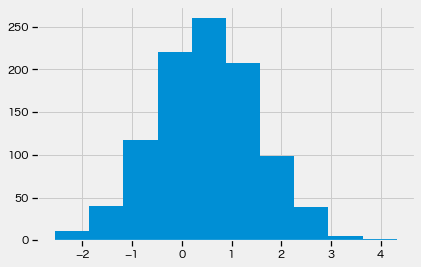
このサンプルを確率分布にしたものが、経験分布です。なので、

def dirac_delta_fn(xx, sigma):
   val = []
   for x in xx:
       if -(1 / (2 * sigma)) <= x and x <= (1 / (2 * sigma)):
           val.append(sigma)
       else:
           val.append(0)
   return jnp.array(val)

def pick_prob_of_x(current_x, samples, sigma=0.5):
    return jnp.sum(dirac_delta_fn([current_x - sample for sample in samples], sigma)) / samples.shape[0]    

def form_empirical_distribution(_from, _to, samples, step=0.01):
    xx = []
    yy = []
    for current_x in np.arange(_from, _to, step):
        y = pick_prob_of_x(current_x, samples)
        xx.append(current_x)
        yy.append(y)
    return xx, yy

xx, yy = form_empirical_distribution(-5, 5, samples)

plt.plot(xx, yy)
plt.show()

dist

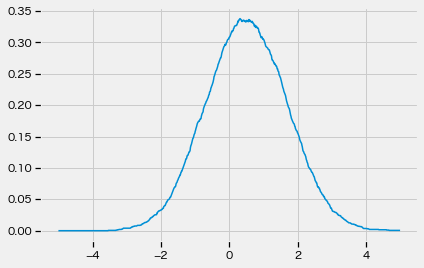
サンプルだけから確率分布を作ることができるのであった。